Fibonacci v Primes: Cage Match!
 Today I decided to more deeply investigate this curious math thing I discovered (for myself) - Plotting the Fibonacci numbers by Prime numbers each by a given modulo. "Fibo-what? Mod-what? So what!", you say. :p
Today I decided to more deeply investigate this curious math thing I discovered (for myself) - Plotting the Fibonacci numbers by Prime numbers each by a given modulo. "Fibo-what? Mod-what? So what!", you say. :p
tl;dr code: slice-seq and slice-seq.R
For the mechanics, I use Perl to produce the data and R to visualize it.
The first is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... The primes are of course: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, ... If you plot them on a graph, each sky-rockets because they are both sequences of bigger and bigger numbers.
What I have been interested in is "boxing in" an infinitely long sequence.
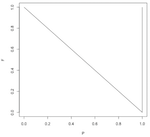
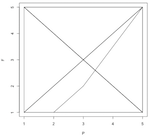
I use modulo (or "clock") arithmetic to keep all numbers within a given range. For example, the friendly 12 hour clock has a "range" of 12, so "13 o'clock" is equal to 1 o'clock and 23:00 == 11PM, etc. My clocks are rectangular...
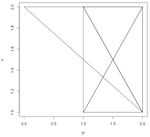
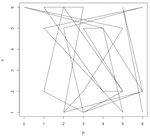
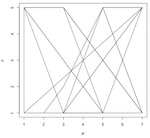
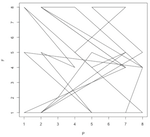
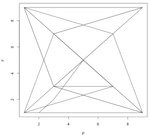
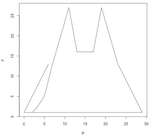
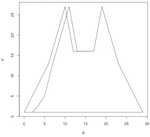
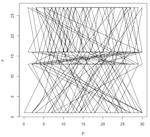
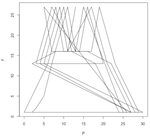
So for each prime number p(n), I find where it would be on the clock, and then do the same for the Fibonacci number of that prime, F(p(n)). Then I make a point and connect it to the previous point. This makes a pattern that grows inside the clock-face box. Some are crazy and random; some are curiously predictable.
Here are the first number pattern pictures, for modulo 2 through 10, with primes below 100 (i.e. 25 primes) plotted:
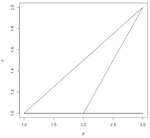
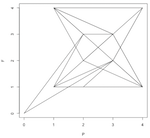
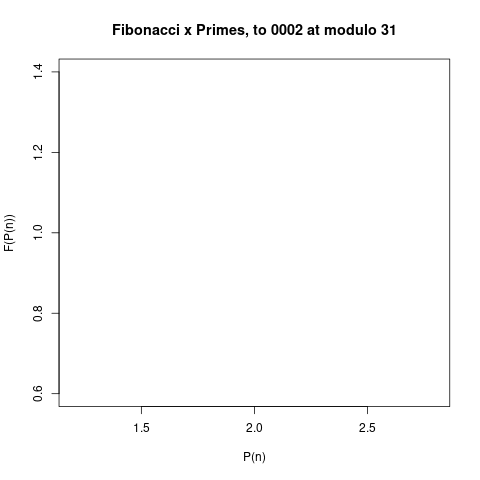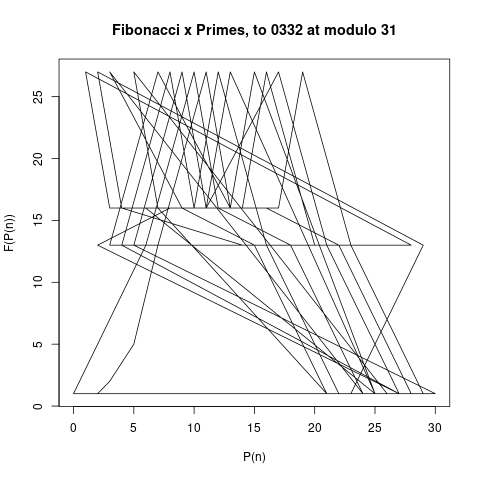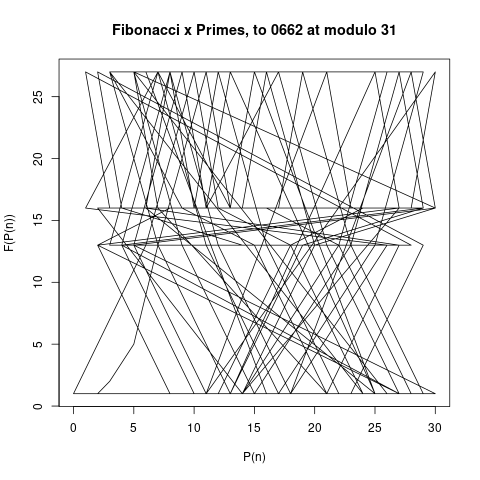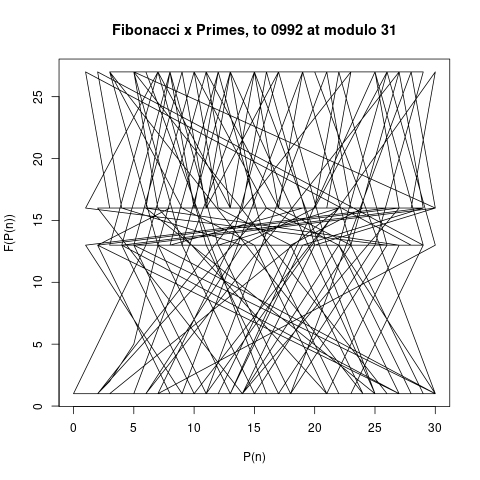
Here are a few pattern pictures where the modulo is only the prime number 31. Each chart shows the "primes below" an increasingly higher number. The first shows primes below 10, then 20, 30, 40, 50, 1000 and the last chart shows primes below 10,000.
These might make a cool "flip-book" PNG animation for math geeks. Maybe I'll do that...
UPDATE
Here is an animated gif of the above:
And here is a table of images showing the x-axis: prime limit up to 100, by 10's, and the y-axis: modulo 2 to 31.
And here is the companion table of images showing the x-axis: prime limit up to 1000, by 100's, and the same y-axis: modulo 2 to 31.
And here are the plots for primes under 10,000, where modulo is again 2 to 31.
Fascinating.